Transformations
Table of contents
Why?
We can use transformations to move objects around in our scene. We can also move our camera around to change the view of the scene. Which of the two we do depends on how many object there are and how big our view plane is.
Homogeneous Coordinates
In homogeneous coordinates, points and vectors are different things. Each point can be expresses as: \(p = p_xi+p_yi + \text{ origin}\).
Points: \((x, y, z, 1)\)
Vectors: \((x, y, z, 0)\), points at infinity.
Subtracting two points gives a vector. Adding a point and a vector gives a point. Adding two vectors gives a vector. But subtracting two vectors is not defined.
2D Transformations
For 2D transformations we use a \(3 \times 3\) matrix. We can use this matrix to translate, rotate and scale our objects.
Scaling
Transformation matrix:
\[\begin{bmatrix} Q_x \\ Q_y \\ 1 \end{bmatrix} = \begin{bmatrix} aP_x \\ bP_y \\ 1 \end{bmatrix} = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix} = SP\]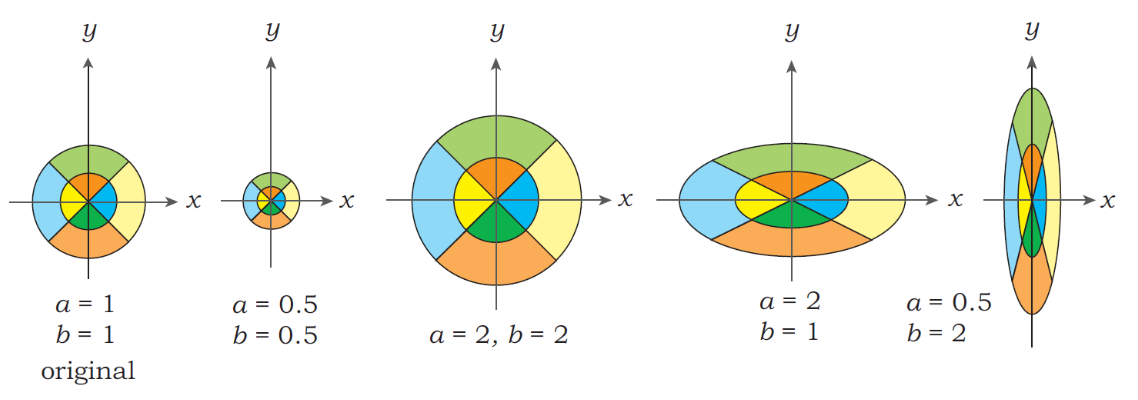
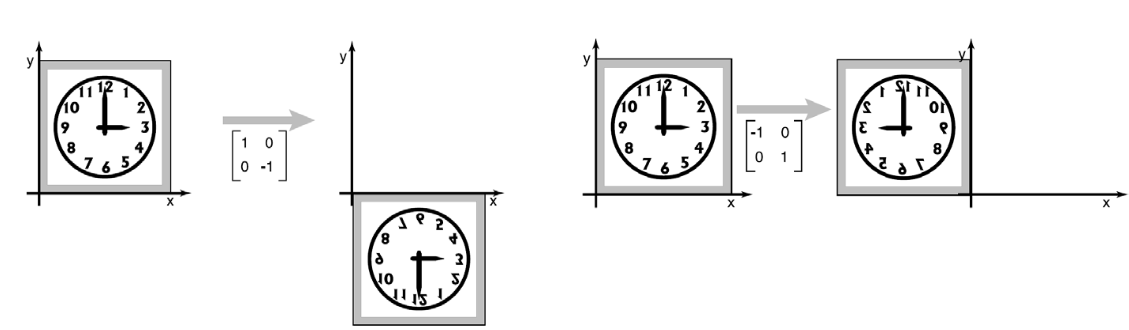
Reflection
This is just a special case of scaling where the scaling factors are negative.
Rotation
\[\begin{bmatrix} Q_x \\ Q_y \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix} = RP\]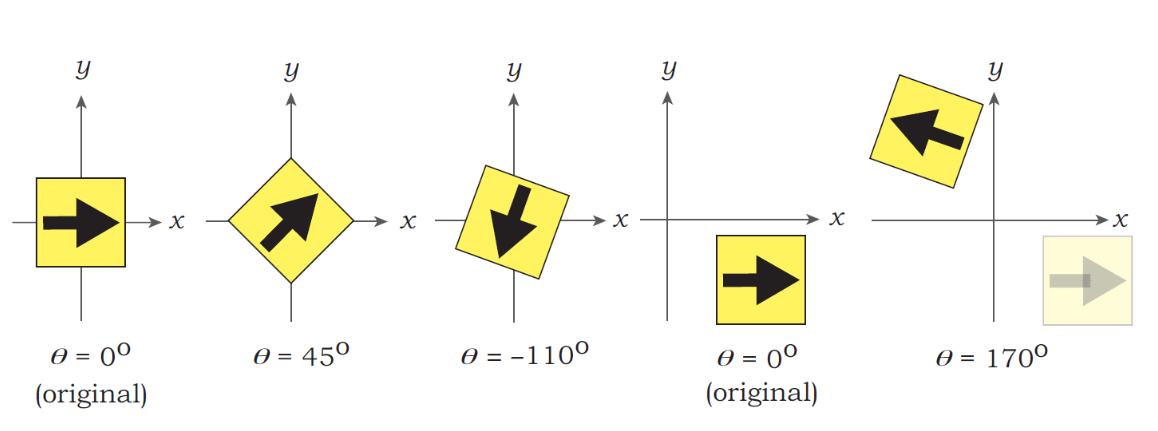
Shear
\[\begin{bmatrix} Q_x \\ Q_y \\ 1 \end{bmatrix} = \begin{bmatrix} P_x + hP_y \\ P_y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & h & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix} = S_hP\]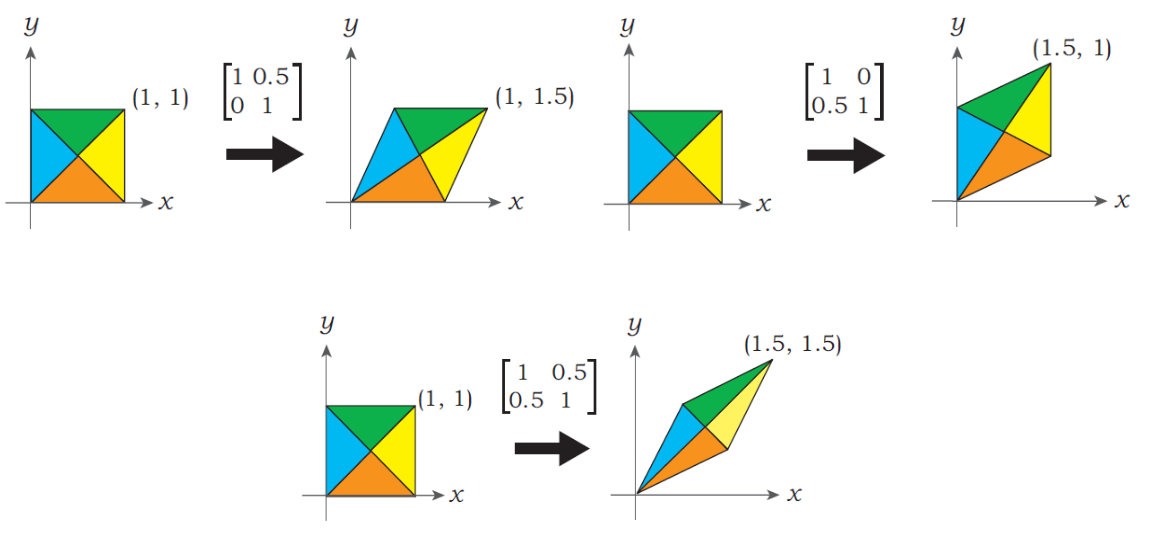
Translation
\[\begin{bmatrix} Q_x \\ Q_y \\ 1 \end{bmatrix} = \begin{bmatrix} P_x + d_x \\ P_y + d_y \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & d_x \\ 0 & 1 & d_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix} = TP\]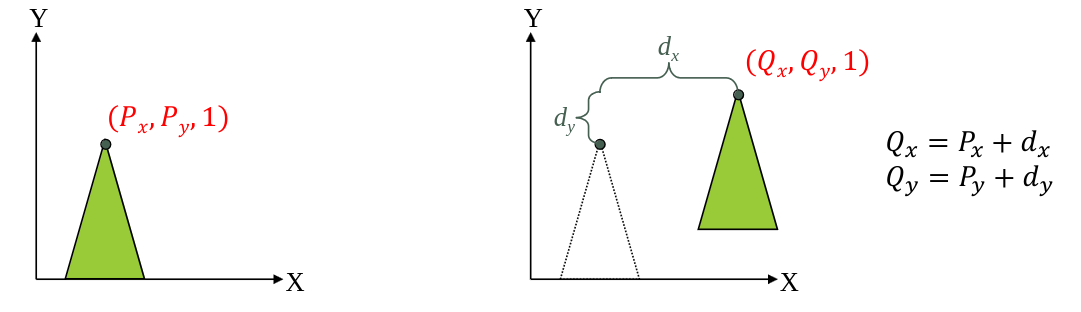
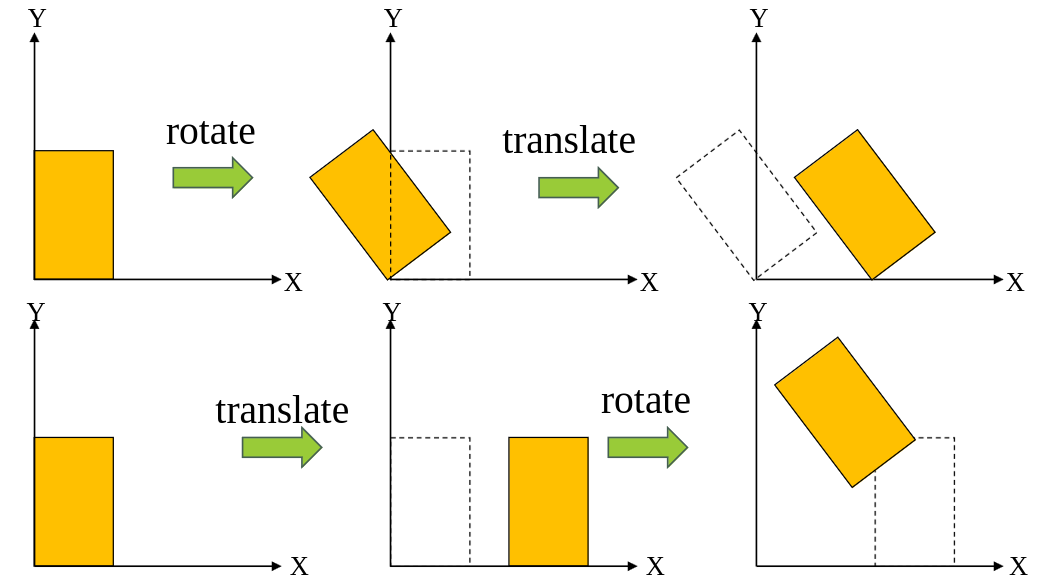
Order
The order in which you apply multiple transformation is important, since a different order can lead to a different result.
Composite Transformations
How do we efficiently apply multiple transformations? Lets say we want to apply a rotation to a non-origin point. We can do this by first translating the point to the origin, then rotating it and then translating it back.
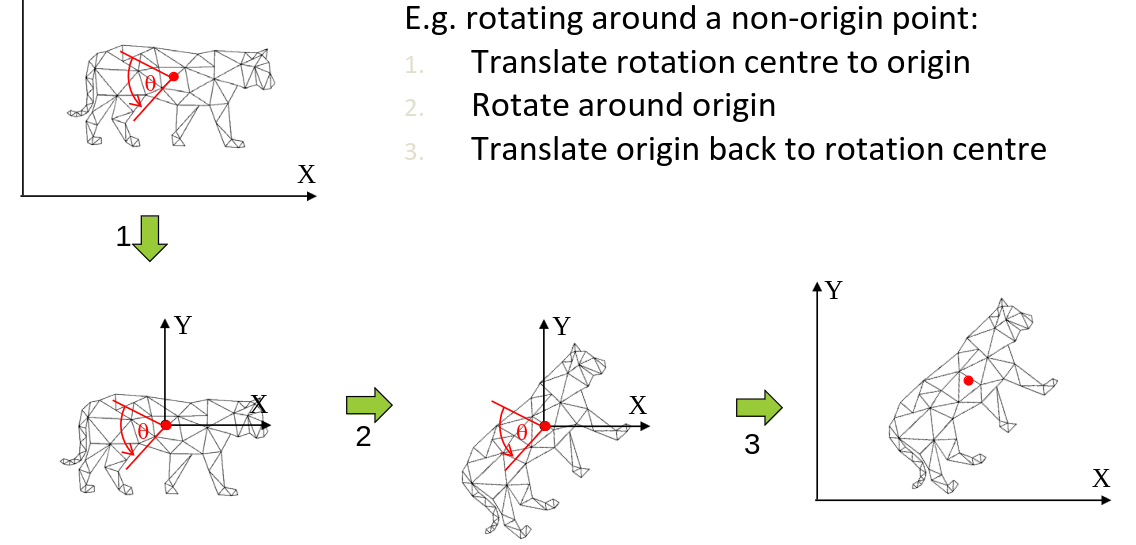
The transformation matrix for this is:
\[Q = \begin{bmatrix} 1 & 0 & T_x \\ 0 & 1 & T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} \cos \theta & -\sin \theta & 0 \\ \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} 1 & 0 & -T_x \\ 0 & 1 & -T_y \\ 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ 1 \end{bmatrix} = T ^{-1}RTP\]But if we apply this matrix we have to do 4 matrix multiplications. We can do this more efficiently by multiplying the matrices together:
\[T ^{-1}RTP = \begin{bmatrix} \cos \theta & -\sin \theta & - \cos \theta T_x + \sin \theta T_y + T_x \\ \sin \theta & \cos \theta & - \sin \theta T_x - \cos \theta T_y + T_y \\ 0 & 0 & 1 \end{bmatrix}\]Inverse Transformations
Scaling:
\[S ^{-1} = \begin{bmatrix} \frac{1}{a} & 0 & 0 \\ 0 & \frac{1}{b} & 0 \\ 0 & 0 & 1 \end{bmatrix}\]Rotation:
\[R^{-1} = \begin{bmatrix} \cos (- \theta) & - \sin (- \theta) & 0 \\ \sin (- \theta) & \cos (- \theta) & 0 \\ 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & \sin \theta & 0 \\ - \sin \theta & \cos \theta & 0 \\ 0 & 0 & 1 \end{bmatrix}\]Shear:
\[s_h^{-1} = \begin{bmatrix} 1 & -h & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{bmatrix}\]Translation:
\[T^{-1} = \begin{bmatrix} 1 & 0 & -d_x \\ 0 & 1 & -d_y \\ 0 & 0 & 1 \end{bmatrix}\]3D Transformations
For 3D transformations we use a \(4 \times 4\) matrix. We can use this matrix to translate, rotate and scale our objects.
Translation
\[\begin{bmatrix}Q_x \\ Q_y \\ Q_z \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & d_x \\ 0 & 1 & 0 & d_y \\ 0 & 0 & 1 & d_z \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = TP\]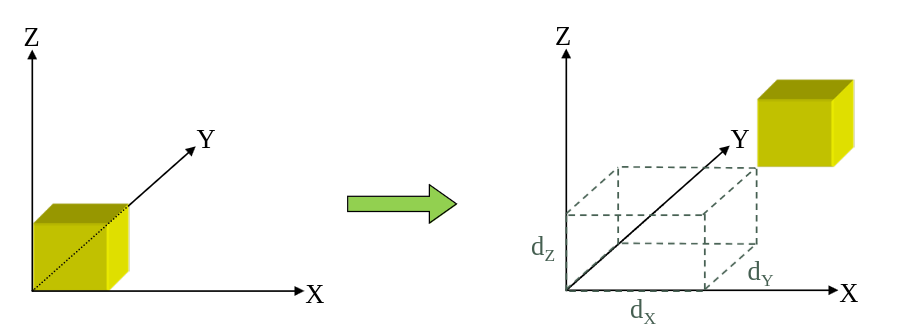
Scaling
\[\begin{bmatrix}Q_x \\ Q_y \\ Q_z \\ 1 \end{bmatrix} = \begin{bmatrix} a & 0 & 0 & 0 \\ 0 & b & 0 & 0 \\ 0 & 0 & c & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = SP\]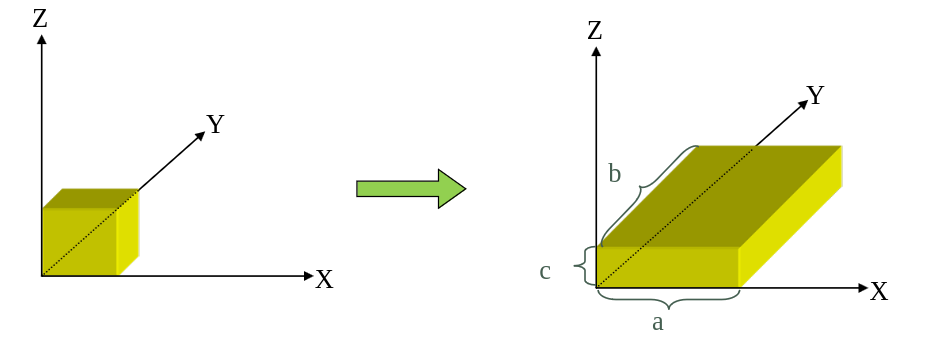
Rotation
The rotation transformation in 3D are always done around a certain axis.
Rotation around the x-axis
\[\begin{bmatrix} Q_x \\ Q_y \\ Q_z \\ 1 \end{bmatrix} = \begin{bmatrix} 1 & 0 & 0 & 0 \\ 0 & \cos \theta & - \sin \theta & 0 \\ 0 & \sin \theta & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = RX\]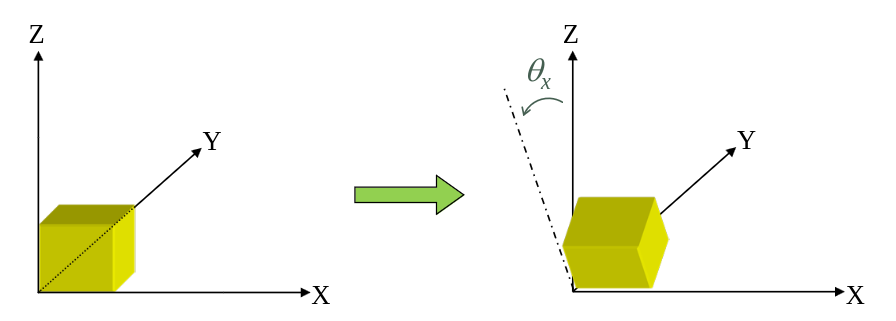
Rotation around the y-axis
\[\begin{bmatrix} Q_x \\ Q_y \\ Q_z \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & 0 & \sin \theta & 0 \\ 0 & 1 & 0 & 0 \\ - \sin \theta & 0 & \cos \theta & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = RY\]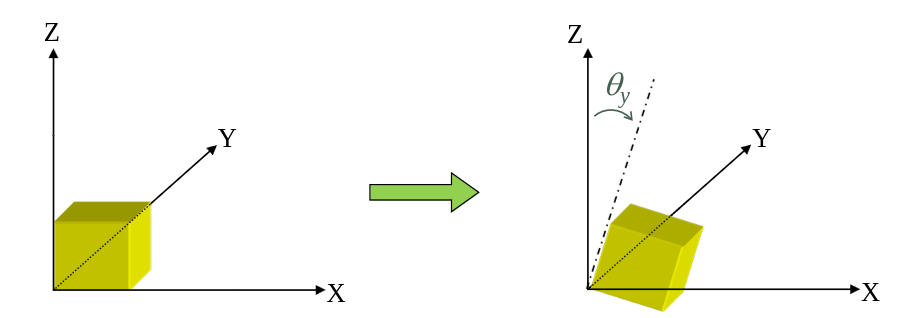
Rotation around the z-axis
\[\begin{bmatrix} Q_x \\ Q_y \\ Q_z \\ 1 \end{bmatrix} = \begin{bmatrix} \cos \theta & - \sin \theta & 0 & 0 \\ \sin \theta & \cos \theta & 0 & 0 \\ 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 1 \end{bmatrix} \begin{bmatrix} P_x \\ P_y \\ P_z \\ 1 \end{bmatrix} = RZ\]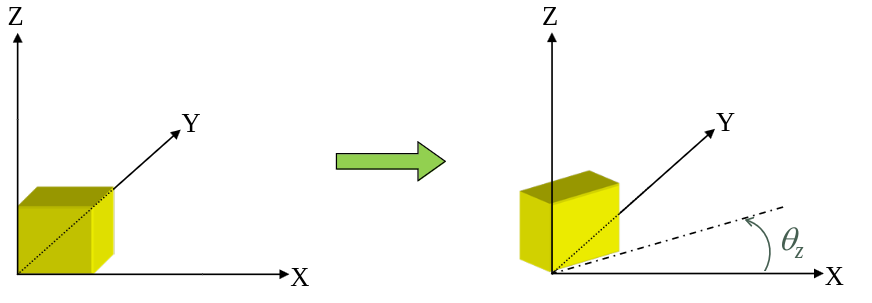
Rotation around an arbitrary axis
We can rotate around an arbitrary axis by first translating the axis to the origin, then rotating around coordinate axis and then translating back.
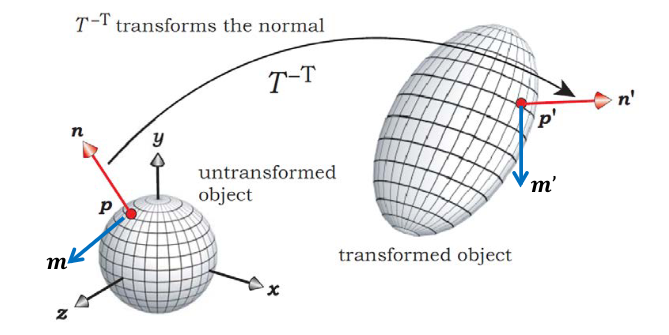
Transforming normal vectors
\[\begin{align} n^Tm &= 0 \\ n^TIm &= 0 \text{ multiplying with the identity matrix gives the same matrix} \\ n^T T^{-1}Tm &= 0 \text{ multiplying with the inverse transformation matrix} \\ (n^T T^{-1}) (Tm) &= 0 \end{align}\]Since we know that \(n^{'T}(Tm) = 0\) we get:
\[\begin{align} n^{'T} &= (n^T T^{-1}) \\ n^{'} &= (n^T T^{-1})^T \\ n^{'} &= (T^{-1})^T n \end{align}\]