Connection Graph

Table of contents

1. Construction a Connection Graph
2. Reading a Connection Graph

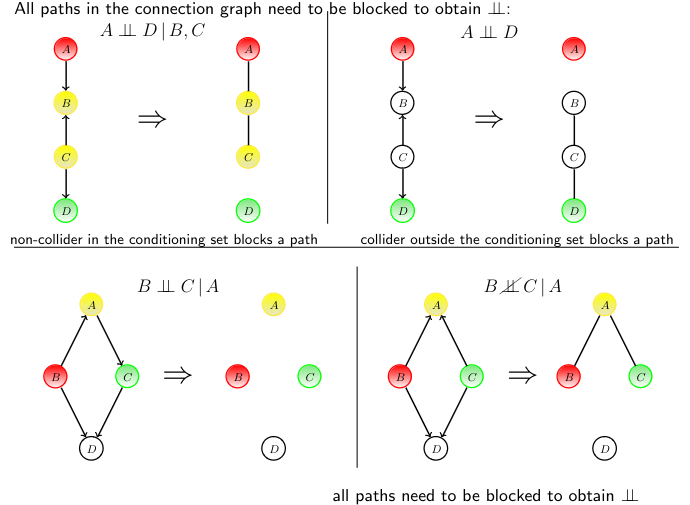
A connection graph is a means to investigate if \(x {\perp \!\!\! \perp} y \mid z\) this is done by:

1. Construct the connection graph to investigate the dependence between ONE pair of variables \(x\) and \(y\).
2. If \(x\) and \(y\) are connected in the connection graph: \(x \not{\!\perp\!\!\!\perp} y\).
3. Repeat for other pairs of variables.

Construction a Connection Graph

If \(z\) is a collider (bottom path) keep undirected links between the neighbours of the collider.

---

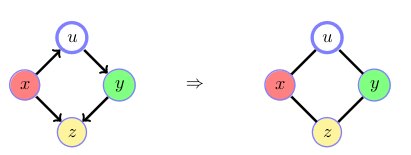
If \(z\) is a descendant of a collider, this could induce dependence so we retain the links (making them undirected)

---

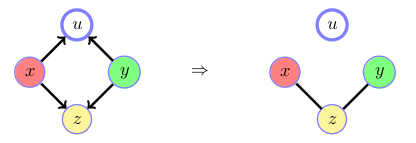
If there is a collider not in the conditioning set (upper path) we cut the links to the collider variable. In this case the upper path between \(x\) and \(y\) is ‘blocked’.

---

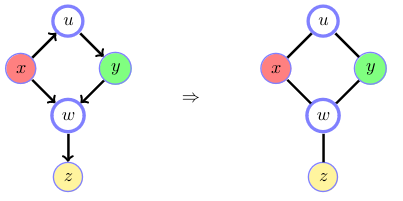
If there is a non-collider which is in the conditioning set (bottom path), we cut the link between the neighbours of this non-collider which cannot induce dependence between \(x\) and \(y\). The bottom path is ‘blocked’.

---

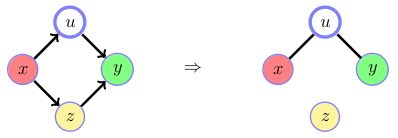
In this case, neither path contributes to dependence and hance \(x {\perp \!\!\! \perp} y \mid z\). Both paths are ‘blocked’.

---

Whilst \(z\) is a collider in the conditioning set, \(w\) is a collider that is not in the conditioning set. This means that there is no path between \(x\) and \(y\), hence \(x\) and \(y\) are independent given \(z\).

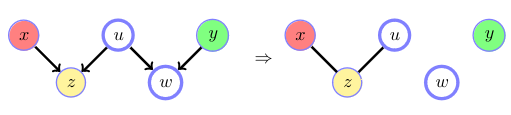
Reading a Connection Graph