Depth of Field
Table of contents
Introduction
The depth of field of a camera is the range of distances over which objects appear to be in focus on the film.
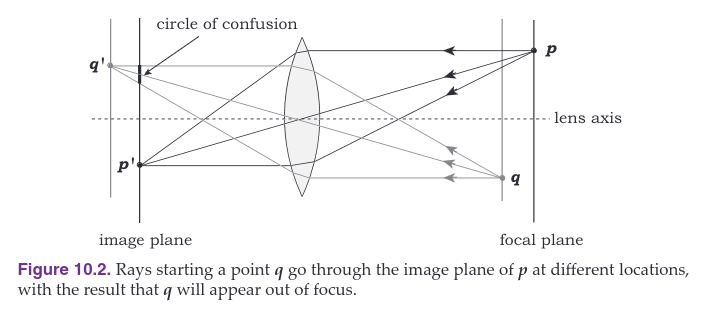
An image \(p\) is in focus since it is imaged on the image plane (image \(p'\)) by the lens. Each focal plane and image plane exist as a matched pair. They are also interchangeable because light can travel in either direction. The different rays from \(q\) hit the image plane of \(p'\) at different places. For rays that only make a small angle with the lens axis, the area they cover is roughly circular and is known as the circle of confusion. If we would place a film on this image plane, \(q\) would be out of focus. The further \(q\) gets from the focal plane of \(p\) (on either side), the larger the circle of confusion becomes, and the more out of focus \(q\) is.
The figure also illustrates that a ray that goes trough the center of the lens is not refracted.
Simulation
To simulate depth of field, we have to simulate the optical properties of the thin lens. First, we represent the thin lens with a disk. Because the disk has zero thickness, we are not quite simulating a real thin lens, which always has finite thickness. The disk is centered on the eye point of the camera and is perpendicular to the viewing direction. Second, we don’t calculate exactly how the light is refracted as it passes through the lens.
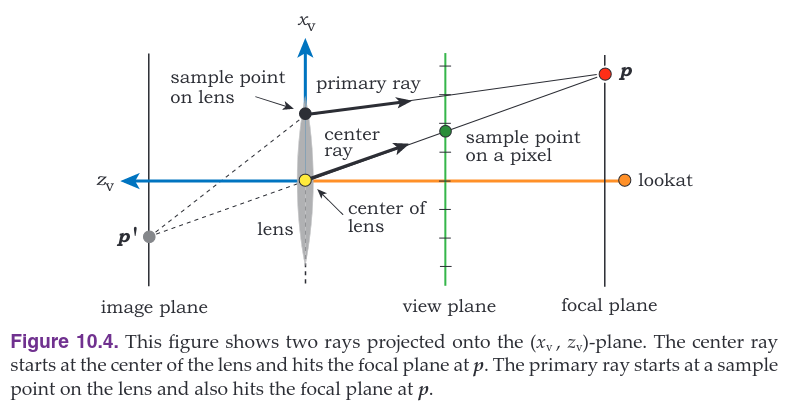
The figure below shows two light paths that join corresponding points on the focal and image planes, where one is straight through the center of the lens and the other is through a sample point on the lens. For each path, we start a primary ray on the lens.
The center ray starts at the eye point at the center of the lens and goes through a sample point on a pixel. In common with pinhole camera, the thin lens camera has the view plane on the opposite side of the lens as the image plane, but this doesn’t invalidate the simulation. The primary ray starts on a sample point on the lens. To simulate depth of field, we perform the following three steps:
- compute the point \(p\) where the center ray hits the focal plane
- use \(p\) and the sample point on the lens to compute the direction of the primary ray so that this ray also goes through \(p\)
- ray trace the primary ray into the scene
The center ray does not contribute to the colour of the pixel; we only use it to find out where \(p\) is. The primary ray is the one that forms the image.