The Bellman equation simplifies our state value or state-action value calculation. If we calculate the \(V(S_t)\) (value of a state), we need to calculate the return starting at that state and then follow the policy forever after. So to calculate \(V(S_t)\), we need to calculate the sum of the expected rewards. 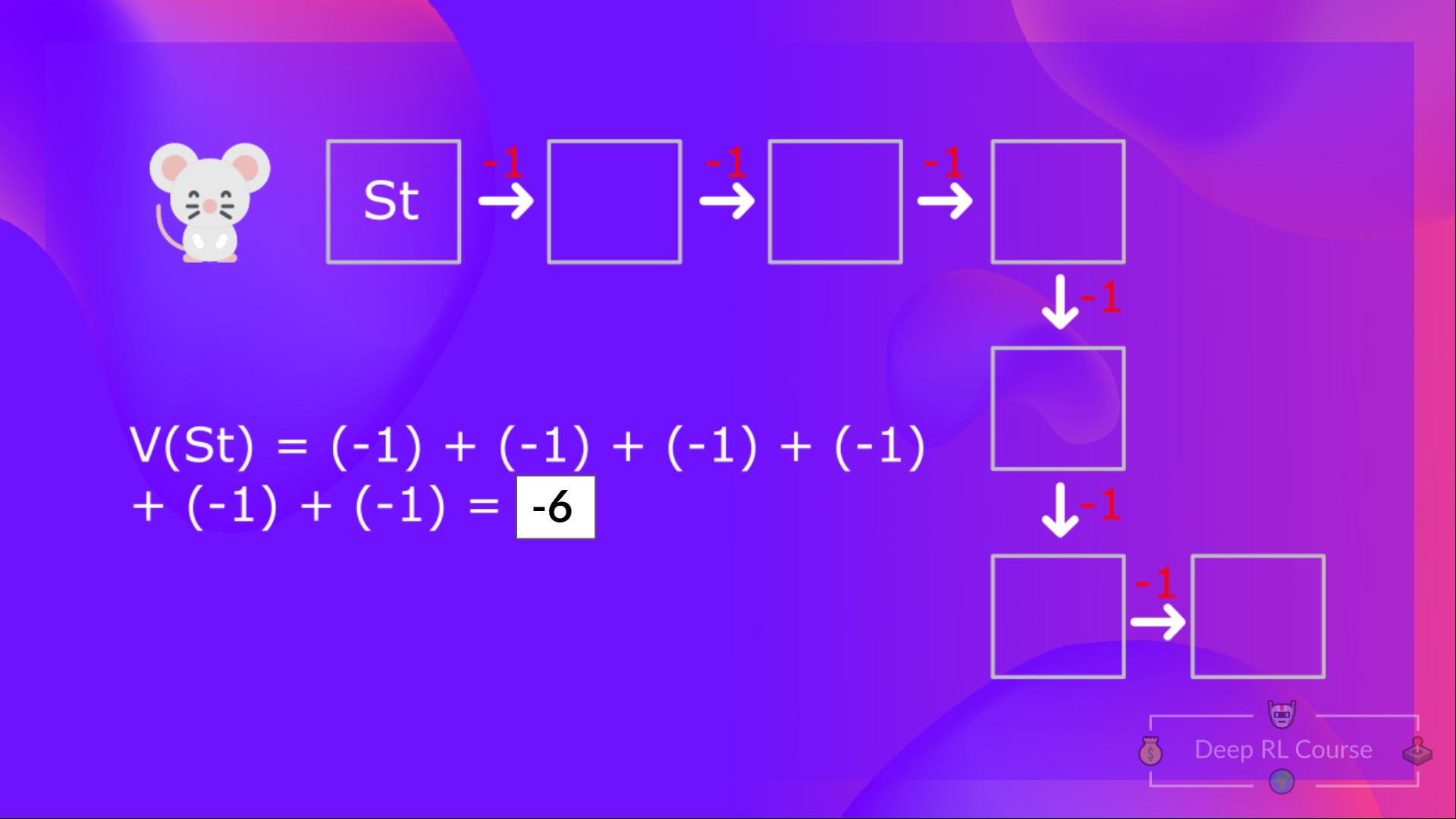Then, to calculate the \(V(S_{t+1})\), we need to calculate the return starting at that state \(S_{t+1}\). 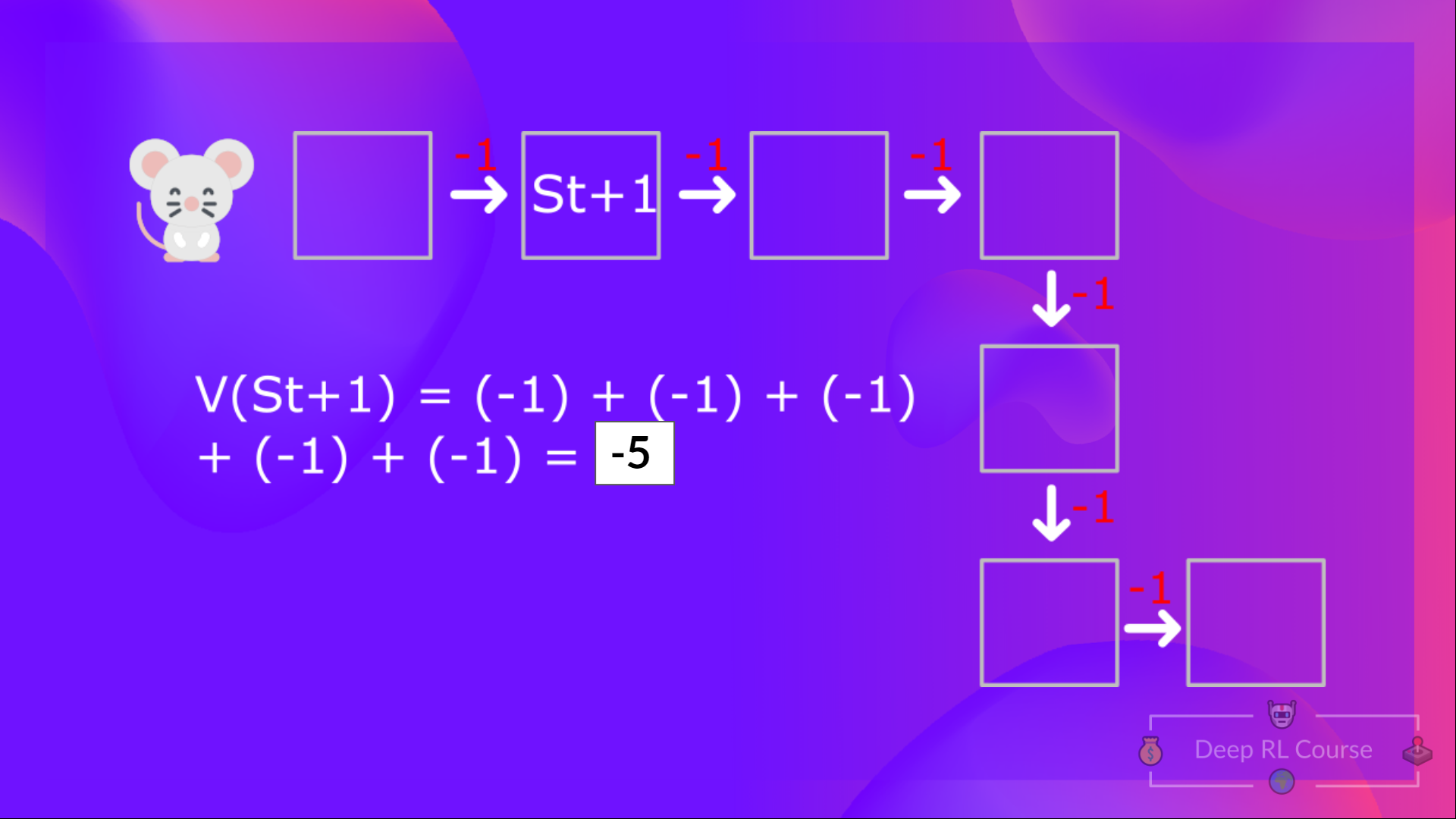We’re repeating the computation of the value of different states, which can be tedious if you need to do it for each state value or state-action value.

Instead of calculating the expected return for each state or each state-action pair, we can use the Bellman equation. The Bellman equation is a recursive equation that works like this: instead of starting for each state from the beginning and calculating the return, we can consider the value of any state as: The immediate reward \(R_{t+1}\)​ + the discounted value of the state that follows (\(\gamma∗V(S_{t+1})\)).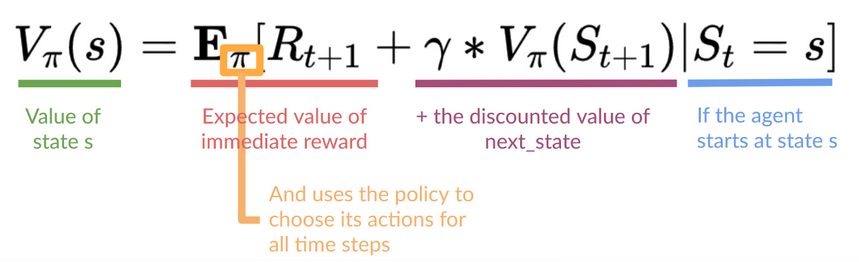

The idea of the Bellman equation is that instead of calculating each value as the sum of the expected return, which is a long process, we calculate the value as the sum of immediate reward + the discounted value of the state that follows.