Logic & Probability

Table of contents

  1. From SAT to WMC
    1. Satisfiability (SAT)
    2. Inference in BN is hard
    3. From SAT to #SAT and WMC
  2. DPLL
  3. Inference via WMC
  4. ProbLog

From SAT to WMC

Satisfiability (SAT)

With a SAT problem we are given a set of boolean variables and a set of clauses of the form \(l_1 \lor \dots \lor l_k\) (k=3, 3-SAT), with each literal a positive or negative variable. The goal is to find an assignment of truth-values to the variables such that all clauses are satisfied.

Example: Lets say we have the following clauses:

\[A \lor B \lor C\] \[\neg A \lor \neg B \lor \neg C\]

A possible solution is \(A = true, B=false, C=true\)

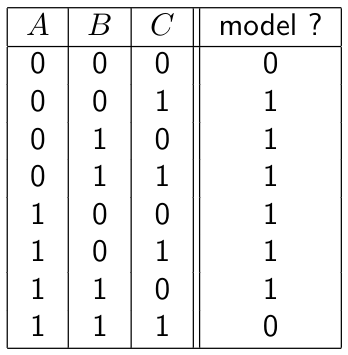
Solutions are called models, one often works with general boolean expressions instead of k-CNF (conjunctive normal form).

All the solutions for this example are: where we have 6 models

sat_example

Inference in BN is hard

Can we encode SAT as a BN inference problem?

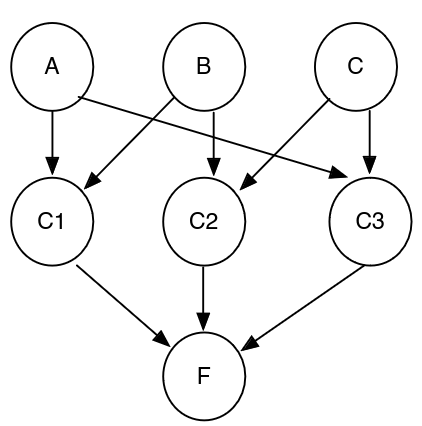
Consider the following example:

\[(\neg A \lor B) \land (\neg B \lor C) \land (A \lor C)\]
  • Assign the priors of \(A, B, C\) as 0.5, and have the other CPTs defined deterministically ( that is, \(C1\) is true iff \(\neg A \lor B\))
  • Then \(p(F) > 0\) iff the formula is satisfiable
  • So, BN inference is at least as had as SAT. (NP-hard)

sat_bn

From SAT to #SAT and WMC

What is the difference between SAT, #SAT and WMC?

  • SAT: doest there exist a model for a logical theory?
  • #SAT: how many models are there for a logical theory? (model counting)
  • WMC: what is the weighted model count?

How do we now go from SAT to #SAT and WMC?

For the previous theory (figure above), there were three models. In the BN, each possible world had a probability of 1/8 and each literal of 0.5 (weight of 0.5). We can now define the weighted model counting problem (WMC) as:

  • Given is a logical theory T (usually in CNF)
  • for each literal \(l\), there is a (non-negative) weight \(w(l)\)

The weighted model count of the theory \(wmc(T)\) is then:

  • \(wmc(T) = \sum_{M \models T} w(M)\) (where \(M\) is model for \(T\), \(M\) is the set of all true literals)
  • \[w(M) = \prod_{l \in M} w(l)\]

DPLL

dpll

  • In a CNF theory \((A \lor \neg B) \land (C \lor D)\), the clauses are the disjunctions, that is, \((A \lor \neg B)\) and \((C \lor D)\)
  • A unit clause contains exactly one literal
  • An empty clause is a disjunction of 0 literals, at least one of which must be true

Example:

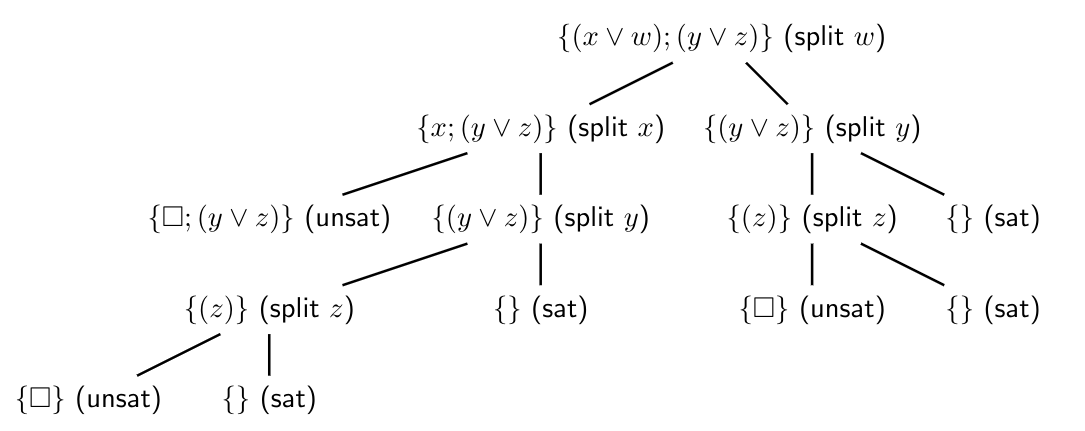
dpll_example

Inference via WMC

We can do this in four steps:

  1. Encode the BN as a boolean expression
  2. Compile the boolean expression into a special data structure (an sd-DNNF)
  3. Turn the sd-DNNF into an arithmic circuit
  4. Perform inference

wmc

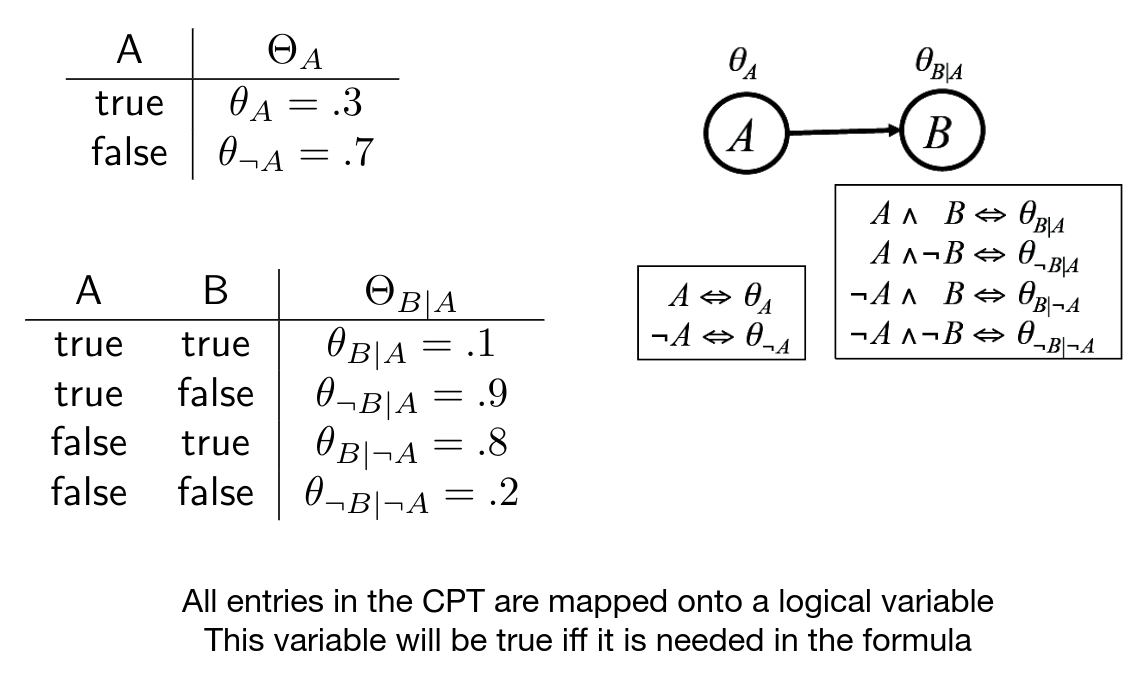
  • We start from the full CPT (with ALL entries, that is for both true and false)
  • Each possible entry/parameter in a CPT is encoded as a logical expression
  • The weights are as follows: \(w(A) = w(\neg A) = w(B) = w(\neg B) = 1\) and \(w(\neg \theta_x) = 1\) but \(w(\theta_x) =\) entry in CPT (as there is no evidence and we are interested in the weighted model count of the complete theory)

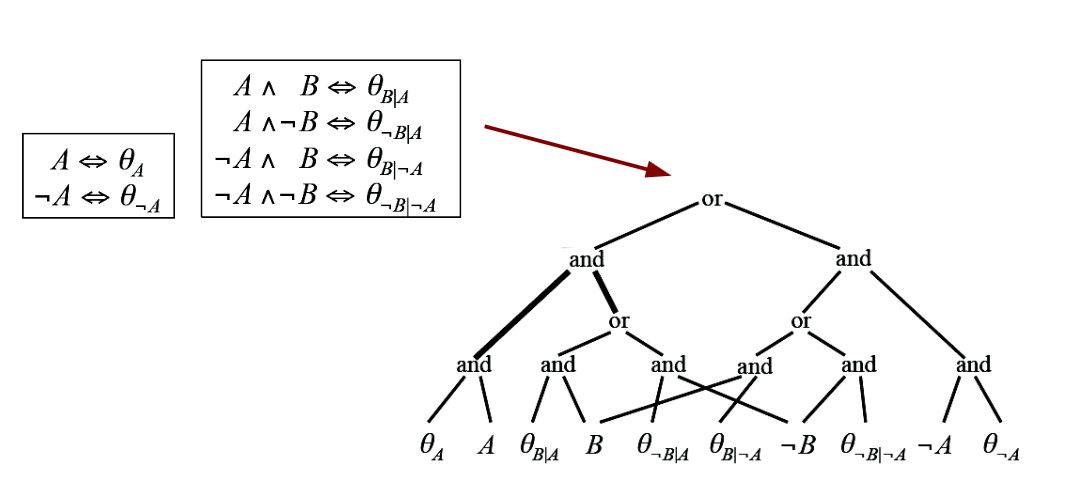
wmc_example

We can now convert it to an arithmic circuit, by replacing AND by multiplication and OR by addition:

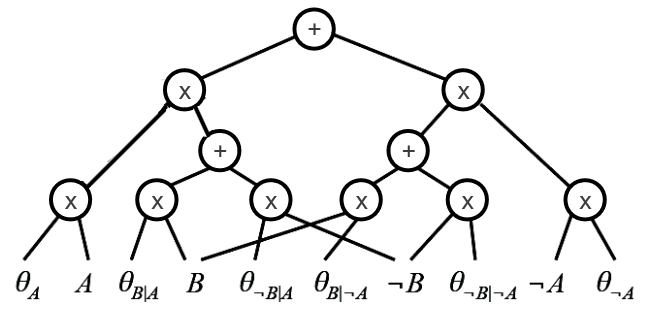
wmc_example_2

ProbLog

In normal Prolog programs, we have facts and rules, the facts are always 100% true. In ProbLog, we give each fact a probability, which is then used to compute the probability of a query.

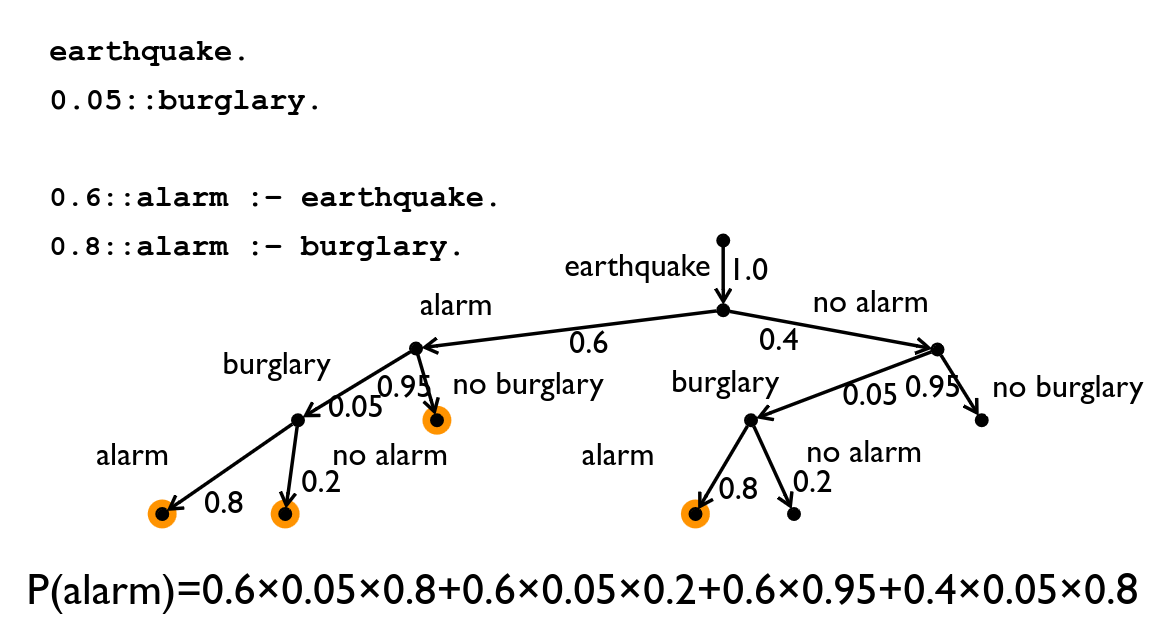
problog

As you can see, OR’s are replaced by addition and AND’s by multiplication.