Hidden Markov Models
Table of contents
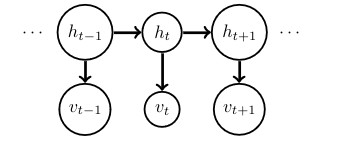
Definition
- A set of discrete or continuous variables \(v_1, \dots, v_T = v_{1:T}\) which represent the observed time-series
- A set of discrete hidden variables \(h_{1:T}\) that generate the observations
The past is independent of the future given the present!
Filtering
Infer \(h_t\) from \(p(h_t \mid v_{1:t})\) which uses the observations up to time \(t\) This is carried out by passing messages up and to the right.
Smoothing
Infer \(h_t\) from \(p(h_t \mid v_{1:T})\) which also uses future observations Combine filtering messages with messages up and to the left.
Viterbi
Infer the most likely hidden sequence \(h_{1:T}\) from \(\arg \max_{h_{1:T}} p(h_{1:T} \mid v_{1:T})\)