Message Passing

Table of contents

Let’s consider the following simple BN with binary variables:

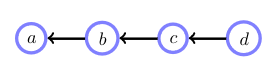
message passing

The joint factorizes as:

\[p(a,b,c,d) = p(a\mid b) p(b\mid c) p(c\mid d) p(d)\]

Let’s now infer \(p(a=0)\)

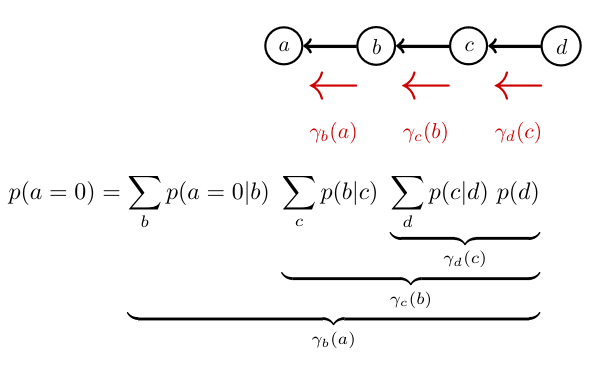
\[p(a=0) = \sum_{b,c,d} p(a=0 \mid b) p(b\mid c) p(c\mid d) p(d)\]
  1. First procedure: Calculate the summation -> we need 7 summations
  2. Second procedure: Push summations inside
\[\text{push d: } p(a=0) = \sum_{b,c} p(a=0 \mid b) p(b\mid c) \sum_d p(c\mid d) p(d)\]

Where \(\gamma_d(c) = \sum_d p(c\mid d) p(d)\). For this we nee 2 summations.

Then we push c inside:

\[\text{push c: } p(a=0) = \sum_{b} p(a=0 \mid b) \sum_c p(b\mid c) \gamma_d(c)\]

Where \(\gamma_c(b) = \sum_c p(b\mid c) \gamma_d(c)\). For this we need 2 summations.

Then we push b inside:

\[\text{push b: } p(a=0) = \sum_{b} p(a=0 \mid b) \gamma_c(b)\]

Where \(\gamma_b(a) = \sum_b p(a=0\mid b) \gamma_c(b)\). For this we need only one summation.

In total we need 5 summations.

A graphical representation of the procedure:

message passing

Loop-cut Conditioning

Problem with multiply connected graphs

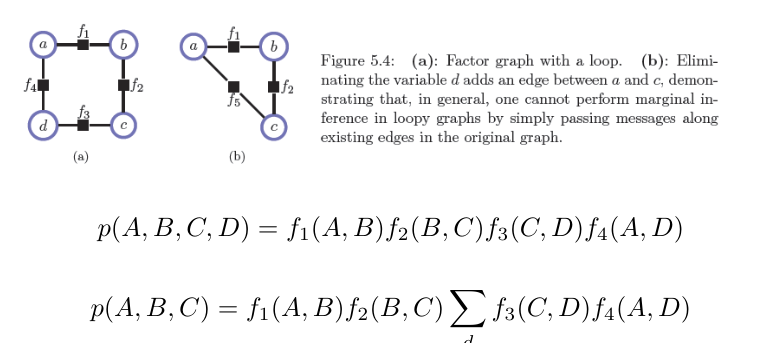
multiply connected

To whom do we send the message? Since marginalizing changes the structure of the factor graph, we can’t just send the message to the parent node.

Loop-cut idea:

  • Identify nodes that when removed result in a singly connected subgraph
  • Do message passing on subgraph
  • Gather results