Barycentric Coordinates

---

Table of contents

1. Why and when are they useful?
   1. Intersection
   2. Texture Mapping
   3. Shading
   4. Morphing and Deformation
   5. Ray Tracing Acceleration Structures

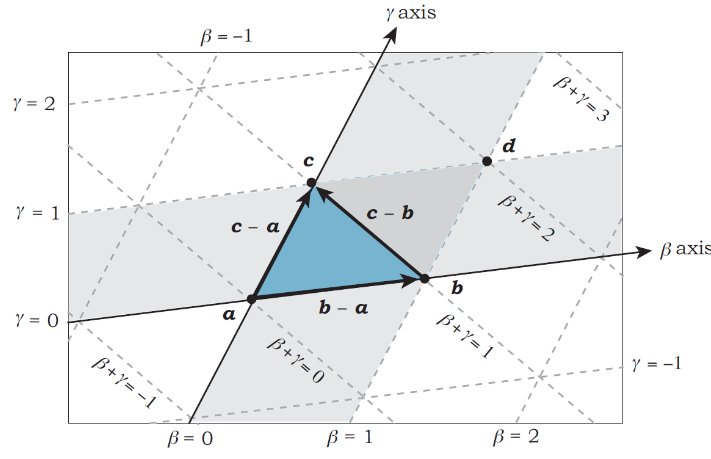
Barycentric coordinates are triples of numbers \((t_1, t_2, t_3)\) corresponding to masses placed at the vertices of a reference triangle \(\Delta A_1 A_2 A_3\). These masses then determine a point \(P\), which is the center of the three masses and is identified with coordinates \((t_1, t_2, t_3)\).

In the example below, each point in the blue triangle can be represented by:

\[p = a + \beta (b - a) + \gamma (c - a)\]

where \(\beta\) and \(\gamma\) are the barycentric coordinates of the point \(p\).

Why and when are they useful?

Intersection

When tracing a ray trough a scene, we need to know if the ray intersects with a triangle. Barycentric coordinates are useful to determine if and where a point is inside a triangle.

Texture Mapping

When applying textures to a surface, barycentric coordinates are used to interpolate between the texel values of the vertices of a triangle. This is important to generate a detailed and realistic texture on objects.

Shading

In shading calculations, especially Gourand and Phong shading, barycentric coordinates are used to interpolate the weighted averages of the normal vectors and colors of the vertices of a triangle. This leads to a smooth shading of the surface.

Morphing and Deformation

With animations or transformations of objects, they are used to create a smooth transition between the geometry different frames. An example is with transforming a mesh.

Ray Tracing Acceleration Structures

They are used in barycentric coordinate hashing to get faster ray-triangle intersection calculations in different acceleration structures.