Light
Table of contents
Radiant Energy
We can think about Radiant energy (Q) as the amount of “photons” (amount of light) that are reflected by a surface. We can do this by measuring the wavelengths since each color has a different wavelength. But this is not what people see when they look at an object. Since the longer you look at the object the more energy the object will reflect, but the object wont get more clearer by looking at it for a longer time.
Radiant Flux
Radiant flux is the amount of radiant energy that passes trough a surface per second. The unit is \(\text{Watt} = \frac{\text{Joule}}{\text{second}}\).
\[\Phi = \frac{dQ}{dt}\]Irradiance
Irradiance (E) is the flux density that arrives at a surface. The unit is \(\text{Watt}/m^2\).
Example
An uniform light source with power P illuminates a small surface A at distance r:
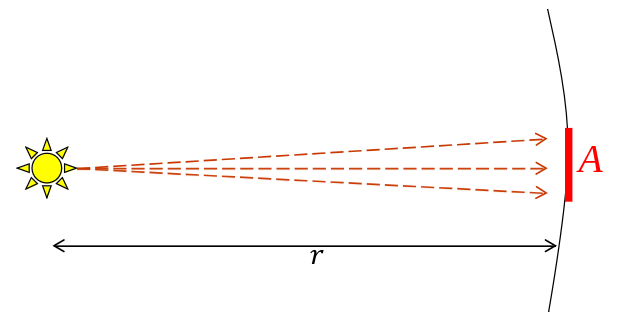
Where \(P_A = P \frac{A}{4 \pi r^2}\) and \(E=\frac{P_A}{A} = \frac{P}{4 \pi r^2}\).
Lets say we know want to calculate the irradiance of a slanted surface:
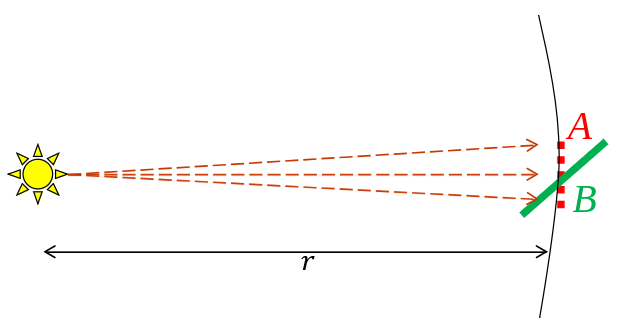
Now we get: \(P_B = P_A = P \frac{A}{4 \pi r^2}\) and \(E=\frac{P_B}{A} = \frac{P_B \cos \theta}{A} = \frac{P \cos \theta}{4 \pi r^2}\).
Environment Lights
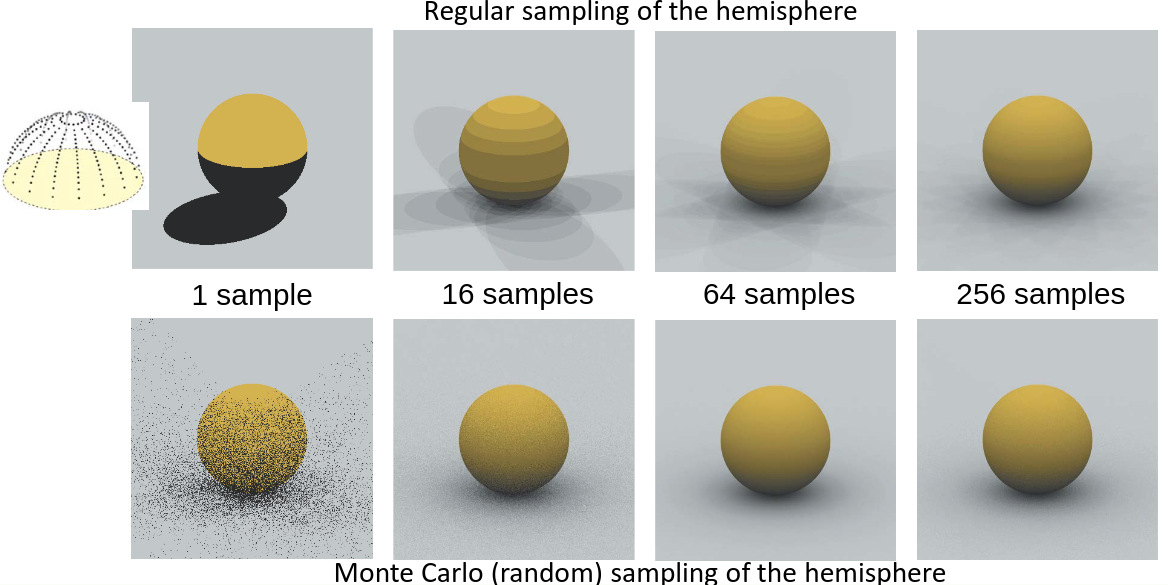
These are lights that surround the entire scene: (directional) light source is modelled as a sphere around the scene.
Write the direct illumination as an integral over hemisphere directions:
\[L_o(p, \omega_o) = L_e(p, \omega_o) \int_{\Omega} f_r(p, \omega_i, \omega_o) L_i(-\omega_i)V(\omega_i) \cos d\omega_i\]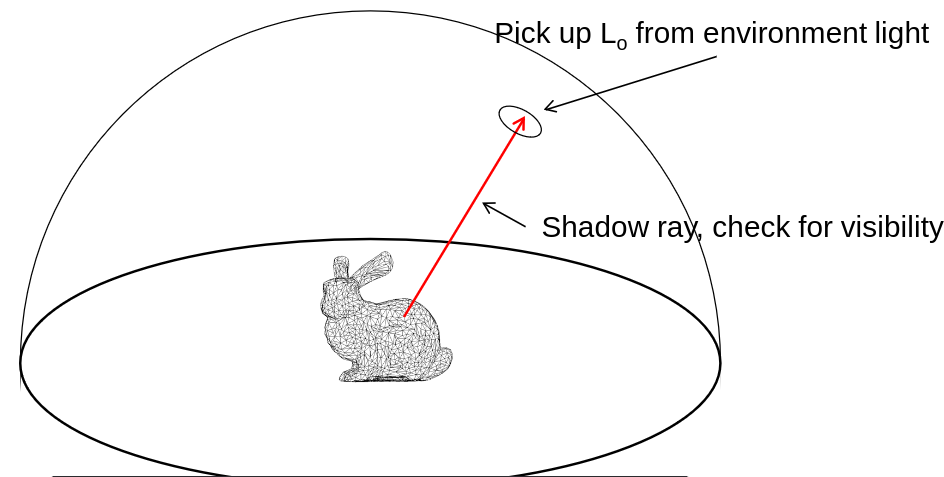
Ambient Occlusion
The intuition is that the amount of light received at a point is proportional to a fraction of the hemisphere that is not occluded towards infinity.
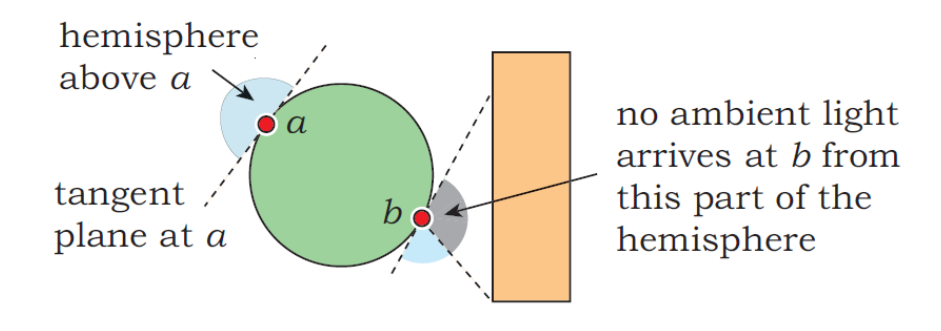
We can formulate this as follows:
\[L_o(p, \omega_o) = [L_e(p, \omega_o)] + \int_{\Omega} f_r(p, \omega_i, \omega_o) L_i(p, \omega_i) \cos\theta_i d\omega_i\]The incoming light has equal intensity from all directions, but some light might be blocked:
\[L_o(p, \omega_o) = L_i \int_{\Omega} f_r(p, \omega_i, \omega_o) V(p, \omega_i) \cos\theta_i d\omega_i\]Diffuse brdf (brdf is a constant):
\[L_o(p, \omega_o) = f_r \cdot L_i \int_{\Omega} V(p, \omega_i) \cos\theta_i d\omega_i\]Where
\(\int_{\Omega} V(p, \omega_i) \cos\theta_i d\omega_i\) can be pre-computed (e.g. at vertices) and stored in a texture. It also only depends on the geometry of the scene, so it can be reused for all materials.