BRDFs

Table of contents

  1. Definition
  2. Properties

Definition

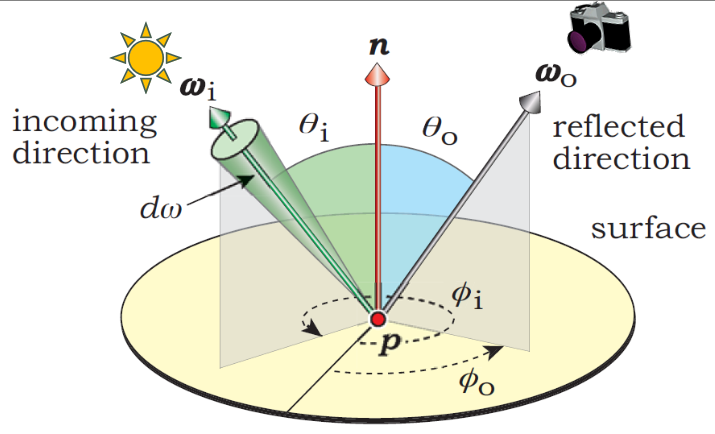
We need a way to precisely describe how light is reflected at surfaces. The bidirectional reflectance distribution function (BRDF) is a function that describes how light is reflected at a surface. It is a function that takes two directions and a point as input and returns a value that ranges from 0 to infinity. An example of a BRDF that is infinite is a mirror.

\[f_r(p, \omega_i, \omega_o) = \frac{dL_o(p, \omega_o)}{L_i(p, \omega_i) \cos \theta_i d\omega_i}\]

where

  • \(f_r\) is the BRDF which has the units \(\frac{1}{sr}\) (inverse steradian)
  • \(\omega_i\) is the incident direction
  • \(\omega_o\) is the outgoing direction
  • \(p\) is the point on the surface
  • \(L_i\) is the incoming radiance
  • \(L_o\) is the outgoing radiance

BRDF

Properties

  • Reciprocity: \(f_r(p, \omega_i, \omega_o) = f_r(p, \omega_o, \omega_i)\)
  • Energy conservation: \(\int_{\Omega} f_r(p, \omega_i, \omega_o) \cos \theta_i d\omega_i \leq 1\) (all outgoing energy is less than the incomping energy, since some energy is absorbed e.g. as heat))
  • Linearity: Materials often need multiple BRDFs to model their reflective properties. In this case, the total BRDF is the sum of the individual BRDFs.