Temporal Difference waits for only one interaction (one step) \(S_{t+1}\)​ to form a TD target and update \(V(S_t)\) using \(R_{t+1}\) and \(\gamma∗V(S_{t+1})\).

The idea with TD is to update the \(V(S_t)\) at each step.

But because we didn’t experience an entire episode, we don’t have \(Gt\)​ (expected return). Instead, we estimate \(G_t\) by adding \(R_{t+1}\)​ and the discounted value of the next state.

This is called bootstrapping. It’s called this because TD bases its update part on an existing estimate \(V(S_{t+1})\) and not a complete sample \(G_t\)​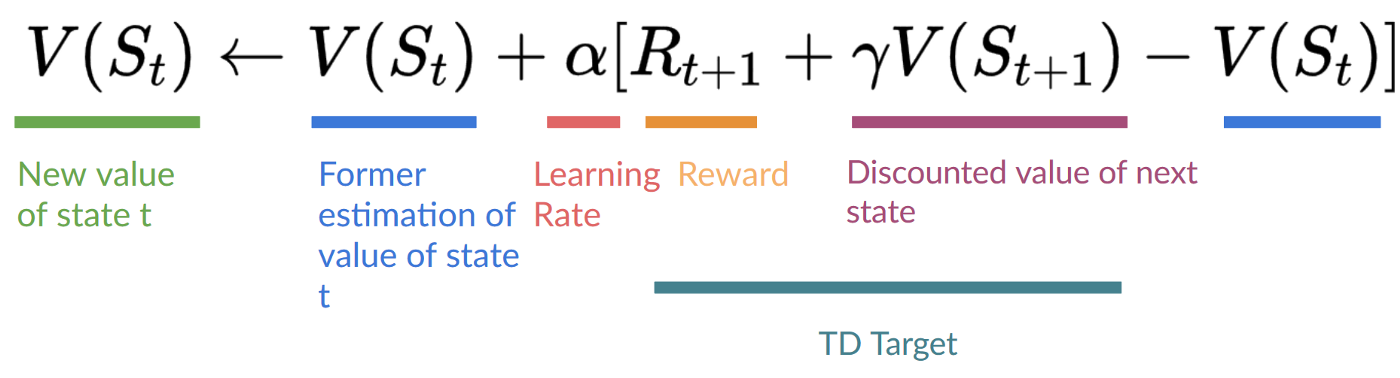. TD approach

Example

TD example

  • We just started to train our value function, so it returns 0 value for each state.
  • Our learning rate (lr) is 0.1, and our discount rate is 1 (no discount).
  • Our mouse explore the environment and take a random action: going to the left
  • It gets a reward \(R_{t+1}=1\) since it eats a piece of cheese
  • We can now update \(V(S_0)\):
  • New \(V(S_0)=V(S_0)+lr∗(R_1+\gamma∗V(S_1)−V(S_0))=0+0.1∗(1+1∗0–0)=0.1\)
  • So we just updated our value function for State 0. Now we continue to interact with this environment with our updated value function.