Variable Elimination

Table of contents

The idea is to calculate a marginal from a joint distribution. We do this by marginalising over all variables except the marginal variables.

E.g.

\[p(f) = \sum_{a,b,c,d,e,g} p(a,b,c,d,e,f,g)\]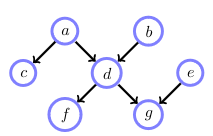

variable elimination

Here we get:

\[\begin{align} p(f) &= \sum_{a,b,c,d,e,g} p(a,b,c,d,e,f,g) \\ &= \sum_{a,b,c,d,e,g} p(f\mid d) p(g\mid d,e) p(c\mid a) p(d \mid a,b) p(a) p(b) p(e) \end{align}\]

Here we can push some summations inside, lets say we use the following order: e,c,b,g,a,d

\[p(f) = \sum_d p(f\mid d) \sum_a p(a) \sum_g \sum_b p(d\mid a,b)p(b) \sum_c p(c\mid a) \sum_e p(g\mid d,e) p(e)\]

But there is probably a better order to do this.

Lets take the order g, e, c, d, b, a:

\[p(f) - \sum_a p(a) \sum_b p(b) \sum_d p(f\mid d) p(d \mid a,b) \sum_c p(c\mid a) \sum_e p(e) \sum_g p(g\mid d,e)\]

Why is this order better? The summation of the last three sums (g, e and c) are all equal to 1. Why is this? This is due that these variables are independent of f, as you can see in the graph above.