To understand the Actor-Critic, imagine you play a video game. You can play with a friend that will provide you with some feedback. You’re the Actor and your friend is the Critic. Actor-Critic image You don’t know how to play at the beginning, so you try some actions randomly. The Critic observes your action and provides feedback. Learning from this feedback, you’ll update your policy and be better at playing that game.

On the other hand, your friend (Critic) will also update their way to provide feedback so it can be better next time.

This is the idea behind Actor-Critic. We learn two function approximations:

  • A policy that controls how our agent acts: \(\pi_\theta(s,a)\)
  • A value function to assist the policy update by measuring how good the action taken is: \(\hat{q}_w(s,a)\)

Now that we have seen the Actor Critic’s big picture, let’s dive deeper to understand how Actor and Critic improve together during the training. As we saw, with Actor-Critic methods, there are two function approximations (two neural networks):

  • Actor, a policy function parameterized by theta: \(\pi_\theta(s,a)\)
  • Critic, a value function parameterized by w: \(\hat{q}_w(s,a)\)

Let’s see the training process to understand how Actor and Critic are optimized:

  • At each timestep, t, we get the current state \(S_t\) from the environment and pass it as input through our Actor and Critic.
  • Our Policy takes the state and outputs an action \(A_t\). actor critic process
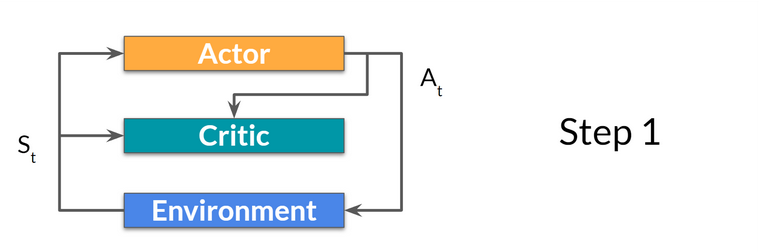
  • The Critic takes that action also as input and, using \(S_t\)​ and \(A_t\)​, computes the value of taking that action at that state: the Q-value. a2c step1
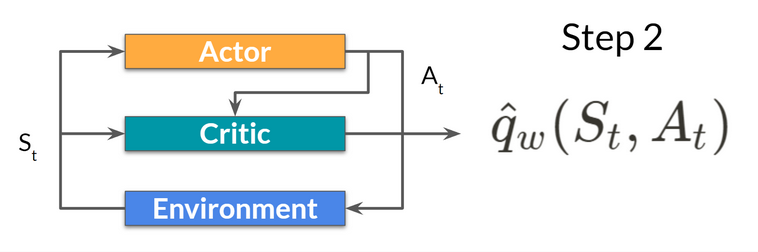
  • The Critic takes that action also as input and, using \(S_t\)​ and \(A_t\), computes the value of taking that action at that state: the Q-value. a2c step2
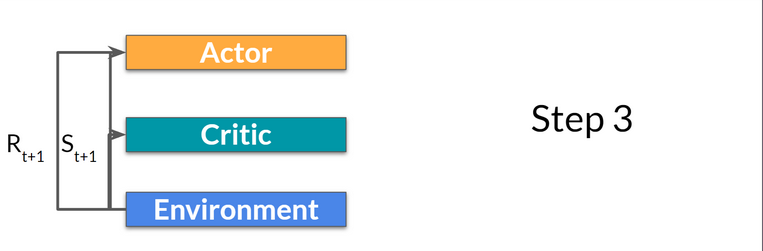
  • The action $A_t$​ performed in the environment outputs a new state \(S_{t+1}\)​ and a reward \(R_{t+1}\) . a2c step3
  • The Actor updates its policy parameters using the Q value. a2c step4
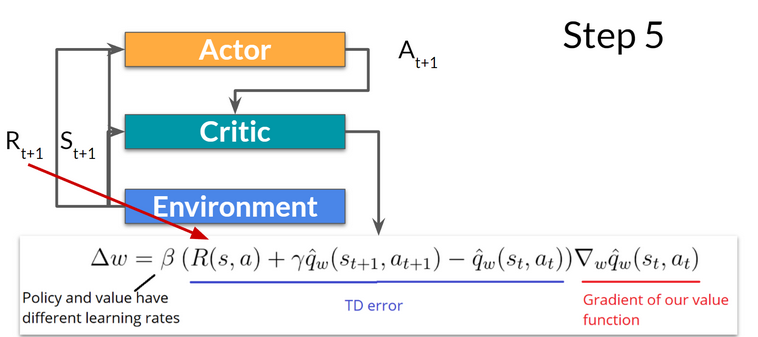
  • Thanks to its updated parameters, the Actor produces the next action to take at \(A_{t+1}\)​ given the new state \(S_{t+1}\)​.
  • The Critic then updates its value parameters. a2c step5

Adding Advantage in Actor-Critic (A2C)

We can stabilize learning further by using the Advantage function as Critic instead of the Action value function. The idea is that the Advantage function calculates the relative advantage of an action compared to the others possible at a state: how taking that action at a state is better compared to the average value of the state. It’s subtracting the mean value of the state from the state action pair: advanced function In other words, this function calculates the extra reward we get if we take this action at that state compared to the mean reward we get at that state.

The extra reward is what’s beyond the expected value of that state.

  • If \(A(s,a) > 0\): our gradient is pushed in that direction.
  • If \(A(s,a) < 0\) (our action does worse than the average value of that state), our gradient is pushed in the opposite direction.

The problem with implementing this advantage function is that it requires two value functions — \(Q(s,a)\) and \(V(s)\). Fortunately, we can use the TD error as a good estimator of the advantage function. advantage function error