Sum-Product Algorithm

---

Table of contents

1. Message schedule
2. Algorithm

Sum-product is a inference algorithm based on message passing for singly-connected factor graphs.

Let’s say we have the following factor graph:

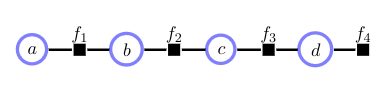
If we want to calculate the marginal distribution of \(A\) we can use the sum-product algorithm:

\[\begin{align} p(a) &= \sum_{b,c,d}p(a,b,c,d) \\ &\propto \sum_{b,c,d} f_1(a,b)f_2(b,c)f_3(c,d)f_4(d) \implies 2^3 \text{ sums} \\ &= \sum_b f_1(a,b) \sum_c f_2(b,c) \sum_d f_3(c,d) f_4(d) \implies 2 \times 3 \text{ sums} \\ \end{align}\]

So we get:

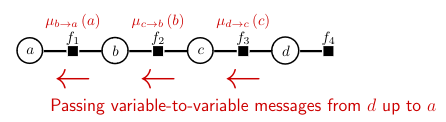
Where

\[\mu_{b\to a}(a) = \sum_b f_1(a,b) \mu_{c\to b}(b) \mu_{d\to c}(c)\] \[\mu_{c \to b}(b) = \sum_c f_2(b,c) \mu_{d\to c}(c)\] \[\mu_{d\to c}(c) = \sum_d f_3(c,d) f_4(d)\]

You can see that we get a time complexity that is linear in the amount of variables instead of exponential.

But what if we want to calculate \(p(c)\)?

\[\begin{align} p(c) &\propto \sum_{a,b,d} f_1(a,b)f_2(b,c)f_3(c,d)f_4(d) \\ &= \sum_b\sum_a f_1(a,b)f_2(b,c) \sum_d f_3(c,d) f_4(d) \end{align}\]

Here we get:

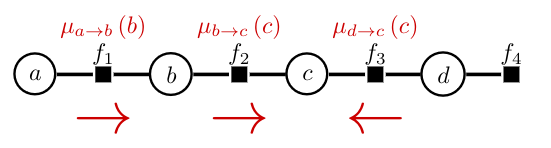
Where

\[\mu_{a\to b}(b) = \sum_a f_1(a,b)\] \[\mu_{b\to c}(c) = \sum_b f_2(b,c) \mu_{a\to b}(b)\] \[\mu_{d\to c}(c) = \sum_d f_3(c,d) f_4(d)\]

As you can see, we need to send messages in both directions!

Message schedule

A message can be sent from a node or factor only when that nodes has received all requisite messages from its neighbours.

Algorithm

In a tree exact inference of all the marginals can be done by two passes of the sum-product algorithm:

1. Pick one node as the root node
2. Initialize:
   • Messages from leaf factor nodes initialized to factors
   • Messages from leaf variable nodes set to unity
3. Step1: Propagate messages from leaves to root
4. Step2: Propagate messages from root to leaves