Bucket Elimination

Table of contents

Bucket elimination is a generalisation of variable elimination that works for any distribution (including non-tree structured distributions). It can be considered as a way to organise the distributed summation when doing marignal variable elimination.

Algorithm

  1. Define an ordering of variables beginning with “marginal variable”
  2. Draw the buckets starting with the “marginal variable” at the bottom
  3. Distribute the potentials over the buckets in the first column:
    • Start with the highest bucket and put all potentials mentioning the variable in the bucket
    • Go to the next bucket and put all REMAINING potentials mentioning the variable in the bucket
  4. Eliminate the buckets:
    • Go to the highest (non-marginalized) bucket and
    • Marginilize the product of the bucket potentials and the bucket message over the bucket variable
    • Send the result (the message) to the highest bucket with bucket variables present in the message
    • Write non-eliminated potentials and the message in the next column
  5. The product of the bucket potentials and bucket messages on the last row, last column is the marginal distribution

Example

Let’s say we have the following model:

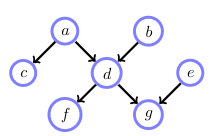
bucket elimination

Where we have:

\[\begin{align} p(f) &= \sum_{a,b,c,d,e,g} p(a,b,c,d,e,f,g) \\ &= \sum_{a,b,c,d,e,g} p(f\mid d) p(g\mid d,e) p(c\mid a) p(d \mid a,b) p(a) p(b) p(e) \end{align}\]

Here we can push some summations inside, lets say we use the following order: e,c,b,g,a,d

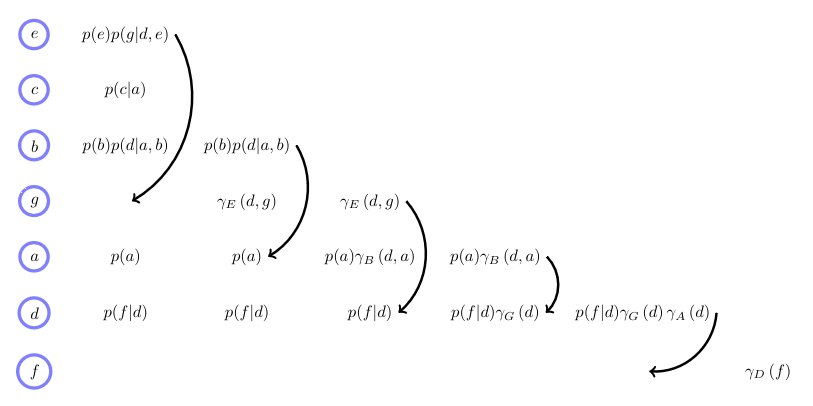
\[p(f) = \sum_d p(f\mid d) \sum_a p(a) \sum_g \sum_b p(d\mid a,b)p(b) \sum_c p(c\mid a) \sum_e p(g\mid d,e) p(e)\]

Follow the procedure in the image below:

  1. F-D-A-G-B-C-E
\[\gamma_E(d,g) = \sum_E p(g\mid d,e) p(e)\] \[\gamma_C() = \sum_A p(c\mid a) = 1\] \[\gamma_B(a,d) = \sum_B p(d\mid a,b)p(b)\] \[\gamma_G(d) = \sum_G \gamma_E(d,g)\] \[\gamma_A(d) = \sum_A p(a) \gamma_B(a,d)\] \[\gamma_D(f) = \sum_D p(f\mid d) \gamma_A(d) \gamma_G(d)\]

bucket elimination

Remarks

  • If you need other marginals you need to re-order the variables and re-run the algorithm. This is not efficient. It would be more efficient to reuse messages, rather than recalculating them each time.
  • Bucket elimination constructs multi-variable messages from bucket to bucket. The storage requirements of a multi-variable message are in general exponential in the number of variables in the message.
  • For singly connected graphs: perfect ordering exists that makes computational complexity linear in the number of variables. However, orderings exist for which bucket elimination will be extremely inefficient.